Backtracking

Recordemos un viejo acertijo: un pastor va paseando con un lobo, una cabra y una gallina. Ahora ha llegado a la orilla de un río y tiene que cruzar al otro lado, y para eso hay una barca, pero tiene un problema: en la barca solo puede llevarse consigo a uno de los animales, así que deberá hacer varios viajes. Sin embargo, los animales no se llevan bien entre sí, y que el pastor los deje desatendidos puede tener consecuencias catastróficas:

• Si el lobo se queda solo con la cabra, el lobo se come a la cabra.
• Si la cabra se queda sola con la gallina, la cabra se come a la gallina (me estoy tomando ciertas libertades en cuanto a definir la dieta de las cabras).

No obstante, el lobo no se comerá a la gallina si se queda solo con ella. ¿Cómo puede el pastor cruzar el río sin que ninguno de sus animales muera devorado?

Si aplicamos un poco de lógica, la solución es evidente:

1. El pastor se lleva a la cabra al otro lado.
2. Vuelve a por otro animal.
3. El pastor se lleva a la gallina o al lobo, indistintamente.
4. Cuando vuelve se trae a la cabra consigo.
5. Deja a la cabra y se lleva el animal que falta.
6. Vuelve solo.
7. Recoge a la cabra y se la lleva al otro lado.

Ahora bien, ¿cómo lo resolvería un ordenador? Evidentemente, no podemos decirle que aplique la “lógica”, ya que es un concepto abstracto y no una serie de instrucciones objetivas y claramente definidas.

Así pues, la alternativa consiste en explorar todas las opciones posibles y descartar aquellos caminos que lleven a una solución incorrecta. A esto se le denomina backtracking o vuelta atrás, que recibe este nombre porque, en resumidas cuentas, vamos realizando, una por una, todas las soluciones posibles yendo paso a paso (generando un árbol de soluciones), y de este modo, cuando llegamos a un paso (nodo) que devuelve una solución incorrecta, volvemos atrás hasta el último nodo de la rama en el que no hayamos explorado todavía todas las posibilidades.

En teoría de grafos, este modo de búsqueda en un árbol (o en un grafo cualquiera) se llama depth-first search, que trata de avanzar por un mismo camino hasta que no podamos avanzar más, y entonces volver atrás hasta el siguiente camino posible. Sin embargo, de momento lo único que nos interesa es la idea de avanzar por una misma solución hasta que se demuestre incorrecta, y entonces probar otra diferente (o bien hasta que lleguemos a una solución válida).

Exploremos entonces cómo resolveríamos, paso a paso, el problema anterior:

1. Desde la situación inicial tenemos tres opciones:
   1. Probamos a llevarnos el lobo, pero descartamos la opción inmediatamente, ya que la cabra se comería a la gallina.
   2. Probamos a llevarnos a la gallina. Descartamos, porque el lobo se comería a la cabra.
   3. Probamos a llevarnos la cabra. De momento siguen todos vivos, así que seguimos en esta rama.
2. Nos llevamos a la cabra. Desde este punto tenemos dos opciones:
   1. Nos traemos de vuelta a la cabra (descartamos, porque volveríamos a la situación inicial).
   2. Nos volvemos con el barco vacío.
3. Volvemos con el barco vacío. Siguen todos vivos.
4. Probamos a llevarnos a la gallina. Siguen todos vivos, así que seguimos explorando esta opción. Ahora tenemos tres opciones:
   1. Nos volvemos con el barco vacío. Descartamos, porque la cabra se comería a la gallina.
   2. Nos traemos a la gallina de vuelta. Descartamos, porque volveríamos a la situación anterior.
   3. Nos traemos a la cabra de vuelta.
5. Nos traemos a la cabra de vuelta. Siguen todos vivos. Tenemos dos opciones:
   1. Nos llevamos a la cabra, pero volveríamos a la situación anterior. Descartamos.
   2. Nos llevamos al lobo.
6. Nos llevamos al lobo. Siguen todos vivos. Dos opciones:
   1. Si nos traemos al lobo o a la gallina de vuelta, estaríamos volviendo a una situación anterior, así que descartamos.
   2. Volvemos con el barco vacío.
7. Volvemos con el barco vacío y solo nos queda una opción: llevarnos a la cabra.

Este proceso se puede representar intuitivamente en forma de árbol:

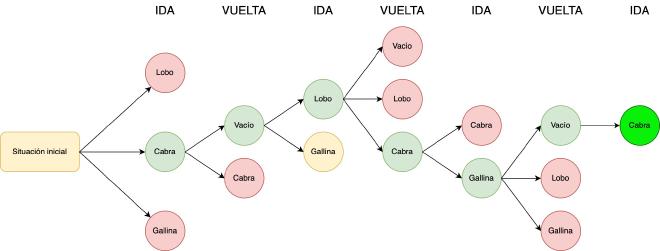
En rojo se indican los pasos que dan lugar a una solución incorrecta. El nodo “Gallina” coloreado en amarillo indica que esa opción no ha sido explorada porque ya hemos llegado a una solución por el otro camino, y por tanto no es necesario seguir buscando.

Un aspecto importante de conocer acerca de la técnica de backtracking es que obtiene soluciones “conformistas”. Como hemos visto en el árbol de la imagen, el algoritmo se detiene inmediatamente en el instante en que halla una solución válida, sea la que sea, por lo que en muchos casos la solución óptima no se puede obtener de ese modo. Evidentemente, el algoritmo se podría modificar para que probase todas las opciones, pero en este caso, la complejidad se dispararía muy por encima de la que ya tenemos (que ya es bastante poco eficiente de por sí), y estaríamos simplemente obteniendo la solución mediante fuerza bruta.

La fuerza bruta es únicamente viable en problemas muy simples o con restricciones extremadamente bajas, y aun así, en la mayoría de casos suele existir una opción alternativa de complejidad mucho menor (aunque pueda resultar más compleja de implementar). Un ejemplo de problema que se puede resolver mediante fuerza bruta es “Exposición de pinturas”, de la OICV 2024 (editorial). La solución propuesta simplemente comprueba todas las posibilidades con complejidad de $O(n^2)$, mientras que la alternativa consiste en realizar una modificación del algoritmo sweep line (Antti Laaksonen, Guide to Competitive Programming, sección 4.2.1) que nos permita obtener la solución óptima en $O(n\log n)$.

Ahora exploraremos cómo podemos obtener la solución del árbol anterior en nuestro código.

Backtracking en pseudocódigo

#

Mediante una serie de abstracciones, la técnica del backtracking se puede utilizar en la mayoría de aplicaciones utilizando una simple función recursiva:

function SOLVE(pasoActual):
    if pasoActual es solución inválida:
        return false
    else if pasoActual es solución válida:
        return true
    else:
        // de momento tenemos una solución parcial, pero
        // todavía no hemos llegado al final

        for pasoSiguiente in pasoActual.ramas:
            // Aquí se itera a través de los posibles siguientes
            // pasos a partir del paso actual

            if SOLVE(pasoSiguiente):
                return true

    return false // el problema no tiene solución

De este modo, podemos buscar la solución desde el paso inicial definiendo el paso o estado inicial como pasoInicial y llamando a SOLVE(pasoInicial). Igualmente, podemos buscar la continuación a una solución parcial desde un paso intermedio mediante SOLVE(pasoIntermedio). La función SOLVE devolverá false únicamente si no existe ninguna solución válida desde el paso inicial que hemos definido, y true en caso contrario (es decir, si se ha hallado una solución válida cualquiera).

La implementación concreta de la comprobación de soluciones válidas e inválidas, así como la definición de pasoActual como una variable concreta, dependen de la propia naturaleza del problema.

Otro ejemplo: el problema de las ocho damas

#

El problema de las ocho damas (o las ocho reinas) es un problema clásico que consiste en encontrar la manera de colocar ocho damas en un tablero de ajedrez estándar (de tamaño 8x8) de modo que no haya dos damas atacándose entre sí —recordamos que dos damas se atacarán si se encuentran en la misma fila, columna o diagonal—. Lógicamente, para obtener una solución válida, en cada fila del tablero debe haber una y una sola dama, puesto que dos damas en la misma fila se atacarían mutuamente. Lo mismo ocurriría en las columnas, aunque en la práctica, lo único que nos interesa es el criterio de las filas. Del mismo modo, también habría que tener en cuenta las diagonales, dado que no puede haber dos damas en la misma diagonal.

Una vez establecidos estos criterios, podemos deducir un algoritmo para colocar las damas en el tablero, yendo fila por fila:

1. Inicializamos $F:=0$, $C:=0$ (siendo $F$ el número de fila y $C$ el número de columna, $0\le F,C<8$).
2. Colocamos una dama en la fila $F$, columna $C$.
3. Comprobamos los ataques entre damas:
   1. Si dos damas se atacan entre sí, incrementamos $C$ en uno: $C\leftarrow C+1$.
   2. Si no, volvemos a la primera columna y saltamos a la fila siguiente: $C\leftarrow 0,F\leftarrow F+1$.
4. Si $F=8$, hemos obtenido una solución válida. Si $F<8$, volvemos al paso 2.

Este planteamiento también se puede extrapolar a un tablero de dimensiones indeterminadas $n\times n$ con $n$ damas, simplemente cambiando la condición del cuarto paso a $F=n$ para parar, y $F<n$ para continuar iterando.

Número de soluciones

#

Una variación común en este tipo de problemas, como la que propone Laaksonen en el libro (págs. 50-51), consiste en calcular el número de soluciones válidas para un problema de este estilo. La solución, más allá de presentar cualquier complicación, solo requiere modificar ligeramente la solución propuesta anteriormente para que, en vez de detener el algoritmo una vez hallemos una posición válida, continúe hasta que se hayan probado todas las combinaciones posibles. De este modo, mantendremos un contador inicializado a cero, que se irá incrementando cuando encontremos una posición correcta, siendo esta finalmente la solución que buscamos.

Ahora, veamos cómo implementar la solución al siguiente problema:

Calcula el número de posiciones posibles en las que $n$ damas se pueden colocar en un tablero de ajedrez cuadrado, de tamaño $n\times n$, de modo que no haya dos damas atacándose entre sí.

Primero, desarrollaremos una solución en pseudocódigo:

fila := 0
contador := 0

function SOLVE(fila):
    if fila == n:
        contador := contador + 1
        return
    else:
        columna := 0
        while columna < n:
            tablero[fila][columna] := dama
            if tablero es posición válida:
                fila := fila + 1
                SOLVE(fila)
            tablero[fila][columna] := vacío
            columna := columna + 1

Así, llamando a SOLVE(fila) o a SOLVE(0) obtendríamos el número de soluciones en la variable global contador.

La dificultad que nos presenta esta solución es la comprobación ambigua “tablero es posición válida”. Formalmente, consiste en comprobar que no haya ninguna otra dama en la fila fila (en cualquier caso, esto no puede ocurrir dada la implementación del algoritmo, que solo coloca una dama por fila), tampoco en la columna columna, ni en las diagonales (esto es, cualquier casilla con fila fila ± i y columna columna ± i, siendo i un entero positivo distinto de cero de modo que la fila y la columna estén dentro del rango $[0,n-1]$).

La propuesta de Laaksonen en el libro consiste en numerar las columnas y las diagonales del tablero (de $0$ a $n-1$ en el caso de las columnas, y de $0$ a $2n-2$ en el caso de las diagonales), y mantener tres vectores col, diag1 y diag2 en los que se indica si hay una dama en una columna concreta, o en las diagonales en ambas direcciones: noreste ($\nearrow$) y sureste ($\searrow$), respectivamente. Las líneas libres se indican con ceros, y las ocupadas con unos.

Por ejemplo, para la siguiente posición en un tablero $4\times 4$:

Primero obtendremos la numeración de las líneas del tablero. Representando el tablero en forma de matrices de tamaño $4\times 4$, en las siguientes matrices $C$, $D_1$ y $D_2$ se indica la numeración de las columnas y diagonales del tablero, y los escaques que contiene cada una:

A partir de la numeración anterior, los vectores col, diag1 y diag2 albergarían los siguientes valores:

Ahora bien, dadas las coordenadas [fila][columna] de una celda cualquiera, ¿cómo sabemos a qué columna y a qué diagonales pertenece? Si observamos atentamente la numeración anterior, obtenemos que el número de columna es simplemente el valor de la coordenada columna. Seguidamente, las diagonales de $D_1$ se obtienen realizando la suma $\mathtt{\text{fila}}+\mathtt{\text{columna}}$, y las de $D_2$ mediante la operación $n-\mathtt{\text{fila}}+\mathtt{\text{columna}}-1$.

Ya tenemos todos los detalles, y podemos implementar la solución en C++:

#include <bits/stdc++.h>
using namespace std;
typedef vector<bool> vb;

void solve(int fila, int n, int& contador, vb& col, vb& diag1, vb& diag2) {
    if (fila == n) {
        contador++;
        return;
    }

    for (int columna = 0; columna < n; columna++) {
        if (!(col[columna] || diag1[fila+columna] || diag2[n-fila+columna-1])) {
            col[columna] = diag1[fila+columna] = diag2[n-fila+columna-1] = true;
            solve(fila+1, n, contador, col, diag1, diag2);
            col[columna] = diag1[fila+columna] = diag2[n-fila+columna-1] = false;
        }
    }
}

int main () {
    int n, contador = 0;
    cin >> n; // recibe el tamaño del tablero

    vb col(n, false), diag1(2 * n - 1, false), diag2(2 * n - 1, false);

    solve(0, n, contador, col, diag1, diag2);
    cout << contador << endl;
    return 0;
}

Problemas

#

Aquí tienes algunos problemas para practicar antes de la próxima sección.

• Two Knights (CSES 1072, solución).

  Explicación (spoiler!)

  Teóricamente, este problema se puede resolver mediante el mismo método que hemos aplicado para resolver el problema de las $n$ damas, pero teniendo en cuenta que el movimiento es diferente al tratarse de caballos, ademas de que solo hay dos figuras en el tablero, independientemente del tamaño de este último. No obstante, en la práctica, una solución recursiva como la que hemos propuesto trataría con unos cálculos demasiado grandes, y mediante un poco de análisis podemos alcanzar una solución lineal para una $k$ cualquiera:

  Las posibilidades para colocar un único caballo en un tablero vacío de dimensiones $k\times k$ es simplemente $k^2$, es decir, el número de casillas. Ahora, si añadimos un segundo caballo, este solo podrá ser colocado en $k^2-1$ posiciones (todas las casillas del tablero menos la que ocupa el primer caballo). De este modo, el número de posibilidades de disponer los dos caballos sobre el tablero es:

  $$n=\frac{k^2(k^2-1)}{2}$$

  Al dividir entre dos eliminamos las posiciones duplicadas, ya que los dos caballos son indistintos uno de otro.

  Sin embargo, no todas las posiciones que hemos considerado son legales (ningún caballo ataca al otro caballo). Hemos de considerar que dos caballos se atacarán si se encuentran en extremos diagonalmente opuestos del mismo bloque de tamaño $2\times 3$ o $3\times 2$ (en esta imagen de GeeksForGeeks se puede visualizar fácilmente). Por tanto, lo único que queda es contar el número de estos bloques que hay en el tablero para determinar el número de posiciones de ataque totales.

  En total, podemos colocar $2(k-1)(k-2)$ bloques de este tipo en un tablero $k\times k$ (explicación en GeeksForGeeks). Esta expresión debe ser multiplicada por dos para tener en cuenta que en cada bloque $2\times 3$ o $3\times 2$ hay dos formas de colocar los dos caballos atacándose entre sí. Finalmente, el número de posiciones de ataque es:

  $$a=4(k-1)(k-2)$$

  Por lo que el número de posiciones válidas, $v$, para una $k$ cualquiera es:

  $$v=n-a=\frac{k^2(k^2-1)}{2}-4(k-1)(k-2)$$

• Chessboard and Queens (CSES 1624; solución).

  Explicación (spoiler!)

  Este problema se resuelve prácticamente igual que el problema de las ocho damas. La única diferencia es que cualquier intento de colocar una dama en una de las “casillas libres” o free squares debe ser rechazado, por lo que no se tendrá en cuenta en el cómputo total.

• Creating Strings (CSES 1622; solución).

  Explicación (spoiler!)

  La solución a este problema se puede implementar recursivamente de modo que, dada una subcadena ya generada, genere continuaciones con los caracteres que todavía no se han utilizado. Sin embargo, este es un caso estrella para utilizar la función estándar next_permutation. Puesto que una cadena de tipo std::string es funcionalmente equivalente a un vector de caracteres, al llamar a la función next_permutation sobre una cadena estaremos generando todas las permutaciones posibles de sus caracteres.

  Al mantenernos en un nivel más elevado de abstracción facilitamos la comprensión del código y ahorramos mucho tiempo en la implementación, que también es un factor clave en la programación competitiva.